ARQUÍMEDES (h. 287 a.C., 212 a.C.)
Rafael V. Martín Algarra (2005)

El momento y el lugar donde un científico encuentra la solución a un problema puede ser el lugar más insospechado, e incluso, para algunos el más inapropiado. Este el caso de Arquímedes, sin duda uno de los científicos más sobresalientes de la Historia, cuyos descubrimientos han sido trascendentales para el desarrollo de la Ciencia.

Su aportación más conocida es el denominado Principio de Arquímedes, que consiguió resolver mientras tomaba un baño, y que se puede considerar el inicio del desarrollo de la hidrostática. Sin embargo, la figura de Arquímedes va más allá del campo de la hidrostática, pues a él se deben importantes principios matemáticos, como los primeros pasos en el desarrollo del cálculo diferencial e integral, y la resolución de principios de la geometría que permitieron desarrollar numerosos inventos y aparatos de ingeniería.

Datos biográficos (ΑΡΧΙΜΗΔΗΣ)

Arquímedes nació hacia el año 287 a.C. en la ciudad estado de Siracusa, en la isla de Sicilia, de tradición y costumbres griegas. Según sus biógrafos siendo muy joven se trasladó a Alejandría, siendo discípulo de destacados sabios de la época como Conón de Samos (280-220 a.C.) astrónomo de la corte de Ptolomeo III, Eratóstenes de Cirene (276-194 a.C.) director de la Biblioteca de Alejandríay Euclides de Alejandría (365-300 a.C.) entre otros.

Años después volvió a su patria, Siracusa, dedicándose al estudio y resolución de múltiples problemas adquiriendo una gran fama. Escribió numerosas obras sobre geometría, mecánica e hidrostática, que han sido reconocidas como tratados de gran interés por numerosos científicos a lo largo de la historia.

Arquímedes murió durante el asalto a la ciudad de Siracusa por las tropas romanas de Marcelo durante la Segunda Guerra Púnica. Aunque no se conoce exactamente cómo murió, se cuenta que estando absorto en la resolución de un problema de geometría, un soldado irrumpió en el estudio de Arquímedes asesinándolo, pues el sabio se resistió a abandonar la resolución del problema matemático en el que estaba inmerso, llegando a recriminarlo por haber desordenado sus esquemas y dibujos. Esta historia se puede encontrar descrita en un bello mosaico de la ciudad de Herculano.

Principio de Arquímedes

Este es el principio por el que es más conocido este gran sabio de la humanidad. La historia cuenta que siendo rey de Siracusa Hierón II, mando a un orfebre de la ciudad que le hiciera una corona. Para ello el rey le entregó al orfebre una determinada cantidad de oro. El orfebre realizó el encargo y entregó la corona, pero el rey, desconfiado, quiso asegurarse de que el orfebre realmente utilizó todo el oro que le entregó.

Arquímedes ya era reconocido como un hombre de gran sabiduría, por lo que Hierón II le pidió que le resolviera este problema, es decir, saber si realmente se había utilizado toda la cantidad de oro para la elabo-ración de la corona o si hubo algún engaño. No sabemos cuanto tiempo transcurrió desde el planteamiento del problema hasta su resolución, pero lo cierto es que mientras Arquímedes se tomaba un baño observó que cuando se introdujo en la bañera una determinada cantidad de agua se desbordó de la misma. La observación de este fenómeno le dio la solución el problema, y según cuentan las crónicas, fue tal su emoción que salió corriendo desnudo de los baños gritando ¡eureka! ¡eureka! es decir ¡lo encontré! ¡lo encontré! (del gr. εúρηκα, encontrar, hallar).

Tomó entonces Arquímedes la corona confeccionada por el orfebre y una cantidad de oro exactamente igual a la utilizada para su fabricación. Por otra parte preparó dos recipientes exactamente iguales contenien-do la misma cantidad de agua hasta su borde e introdujo en uno la corona y en el otro el oro. Observó enton-ces que el agua que se derramaba del recipiente que contenía la corona era diferente que el del otro recipiente demostrando el fraude del orfebre, pues sustituyó parte del oro que el rey le dio por plata. La razón es hoy bien conocida, pues la densidad de ambos metales es diferente, y el volumen que ocupan es diferente, pues el oro tiene una densidad de 19,3 g/cm3, mientras que la de la plata es de 10,5 g/cm3. Por esta razón se utilizó para determinar la proporción de los metales que componen algunas aleaciones, es decir para conocer su ley.

A partir de esta observación se establece el Principio del Empuje Hidrostático o Principio de Arquímedes que se enuncia del siguiente modo: Todo cuerpo que se sumerge en un líquido experimenta un empuje de abajo hacia arriba igual al peso del volumen del líquido desalojado.
Este principio tiene una gran importancia práctica para la flotación y estabilidad de los buques, algo que ya planteó el propio Arquímedes con su tratado Sobre el equilibrio de los cuerpos flotantes; pero además se aplica a los globos aerostáticos y se utiliza para la corrección de las pesadas de precisión.

Tornillo de Arquímedes

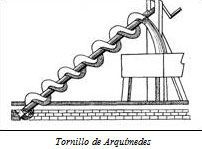Entre los numerosos inventos de Arquímedes también es destacable el tornillo sin fin, que originariamente fue utilizado como sistema para sacar agua de la sentina de los barcos, y posteriormente como sistema para elevar agua, harina o grano.
Este sistema sigue siendo en la actualidad utilizado en múltiples ingenios y maquinarias como las bombas de tornillo sin fin para el desplazamiento de sólidos y líquidos, especialmente para sustancias viscosas como por ejemplo en el trasvase de grandes cantidades de pastas y cremas en la industria farmacéutica.

Espiral de Arquímedes

En un escrito titulado Sobre las espirales Arquímedes escribió:
“Si una línea recta que permanece fija en un extremo, se le hace girar en el plano con velocidad constan-te, hasta hacerla volver de nuevo a la posición de la que ha partido, y junto con la recta que gira, se mueve un punto sobre la recta, también a velocidad constante iniciando su movimiento desde el extremo fijo, el punto describe en el plano una espiral”.
Este efecto se puede observar en la figura adjunta.

Y también:
“El área de la espiral en su primera vuelta es igual a la tercera parte del área del círculo que la envuel-ve”
Esta espiral es la que se conoce como Espiral de Arquímedes, de la que pudo establecer que el radio vec-tor de una espiral es proporcional a su ángulo, es decir, la ecuación es:

En esta expresión r es la distancia al origen, a una constante y  el ángulo girado. Este descubrimiento algunos autores se lo atribuyen también a su amigo y maestro Conón de Samos.

Cráter de Arquímedes

La astronomía también decidió honrar a este gran sabio dando nombre a varios accidentes geográficos lunares. El Cráter de Arquímedes tiene un diámetros de aproximadamente 80 Km., siendo el cráter más gran-de del Mar de las Lluvias o Mare Imbrium.

Montes de Arquímedes

A su vez, como consecuencia del impacto del meteorito que formó el cráter, se produjo la eyección de materiales creándose una formación montañosa que se denominó Montes de Arquímedes o Arquimedianos

Rima o Fisura de Arquímedes

Y finalmente, en dirección sur sureste existen varias grietas de gran longitud que se conocen como Rima o Fisura
de Arquímedes. De los viajes espaciales que han tenido por destino la Luna sólo dos alunizaron en las proximidades de esta zona. El primero de ellos (14/09/1959) la nave soviética Luna 2 que no llevaba tripula-ción y el segundo fue un vuelo tripulado de la NASA, el Apolo 15 (30/07/1971).

ANEXO: ALGO MÁS SOBRE ARQUÍMEDES

Geometría: el número pi (π)
Son numerosos los estudios, reflexiones y principios que estableció sobre las figuras geométricas y el espacio que estas ocupan
Entre ellos podemos destacar la aproximación que hizo del número pi , estableciendo que su valor se encuentra comprendido entre 221/71 (3,1126) y 22/7 (3,1428), tras realizar diversos estudios con una circun-ferencia en la que se inscriben o circunscriben diferentes polígonos regulares tal y como muestra la figura, estableciendo que la relación entre el perímetro de la circunferencia y el diámetro de la misma es un número constante, es decir pi.

Geometría: el número pi (π)
Son numerosos los estudios, reflexiones y principios que estableció sobre las figuras geométricas y el espacio que estas ocupan
Entre ellos podemos destacar la aproximación que hizo del número pi (π), estableciendo que su valor se encuentra comprendido entre 221/71 (3,1126) y 22/7 (3,1428), tras realizar diversos estudios con una circun-ferencia en la que se inscriben o circunscriben diferentes polígonos regulares tal y como muestra la figura, estableciendo que la relación entre el perímetro de la circunferencia y el diámetro de la misma es un número constante, es decir pi.

Igualmente trabajó con figuras tridimensionales y son famosos sus estudios sobre las esferas demostrando que la superficie de la misma es cuatro veces la de uno de sus círculos máximos; también calculó la superficie de semiesferas y poliedros de distintas formas, así como sus estudios sobre las espirales ya comentados.

Tal era su dedicación a estos estudios sobre las figuras geométricas, que en su tumba ordenó que grabaran uno de sus teoremas que describía la relación que existe entre un cilindro y la esfera que en éste puede inscri-birse, el problema al cual le atribuía gran importancia era el de demostrar que «El volumen de una esfera inscrita en un cilindro es igual a 2/3 del volumen del cilindro» tal y como muestra la figura.

Ingeniería y mecánica.

También es célebre la frase que se atribuye a Arquímedes “dadme un punto de apoyo y moveré el mundo” a partir de la cual podemos decir que nació el principio de la palanca, utilizado en las construcción de distintas máquinas de guerra con las que, según las crónicas de la época, permitieron resistir al rey Hierón II el asalto a la ciudad de Siracusa de las tropas romanas de Marcelo.

A Arquímedes también se debe la invención de algunas poleas y ruedas dentadas precursores de los en-granajes. También es conocida la historia del empleo de espejos cóncavos (espejos ustorios) que se utilizaron en la defensa de Siracusa. Con ellos se concentraba la luz del sol sobre las velas de los barcos enemigos in-cendiándolos.

Para finalizar cabe destacar la admiración que este sabio griego ha despertado en numerosos personajes científicos relevantes, pues sin duda fue un hombre muy adelantado a su tiempo y con una visión científica fuera de lo común dados los recursos disponibles.

Bibliografía

Enciclopedia Universal Ilustrada Europea-Americana, 2. Espasa Calpe.

Diccionario de Física. 2ª Edición. Labor, S.A. 1967 

Enciclopedia Universal Espasa Calpe. Grandes Científicos de la Humanidad. Espasa, 1998. 

Chris Rorres. Drexel University

Archimedes. Visitar Web Departamento de Ciencias Universidad de Drexel

Visitar Web: Gacetilla Matemática: Historias. Arquímedes de Siracusa

Visitar Web: Espiral de Arquímedes, Espiral de Arquímedes II

A. Pérez. Espirales en la Historia de las Matemáticas. En: Divulgamat.

Rafael V. Martín Algarra
Universidad CEU Cardenal Herrera

Ana Mª Martín Algarra
I.E.S. Mariano Baquero Goyanes
Murcia